Induksi matematika
Induksi matematika
Induksi matematik merupakan pembuktian deduktif, meskipun namanya induksi. Induksi matematik atau disebut juga induksi lengkap sering digunakan untuk membuktikan pernyataan-pernyataan berkenaan bilangan asli.
Pembuktian cara induksi matematik ingin membuktikan bahawa teori atau sifat itu benar untuk semua bilangan asli atau semua. Caranya ialah dengan menunjukkan bahwa pernyataan itu benar untuk n = 1 (atau S(1) adalah benar), kemudian diasumsikan bahwa bila pernyataan itu benar untuk n = k (bila S(k) benar) maka pernyataan itu turut benar untuk n = k +1 (atau S(k+1) benar).
Contoh
Buktikan bahwa jumlah n nomor ganjil pertama adalah n2.
Penyelesaian :
Bentuk Matematis dari pernyataan diatas adalah :

S(n) = 1 + 3 + 5 +\cdots + 2n-1 = n^2
-
Untuk n = 1, memang benar –> S(1) = n2 = (12) = 1.
-
Andaikan pernyataan ini benar untuk n = k, yaitu
- , Akan dibuktikan benar pula untuk n=k+1, yaitu
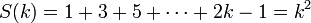
S(k) = 1 + 3 + 5 +\cdots + 2k-1 = k^2
![1 + 3 + 5 +\cdots + 2k-1 + [2(k+1) - 1] = k^2 + 2(k+1) - 1](http://upload.wikimedia.org/math/e/e/e/eee0251b6c418fa37683efd4a9847bff.png)
1 + 3 + 5 +\cdots + 2k-1 + [2(k+1) - 1] = k^2 + 2(k+1) - 1

\; = k^2 + 2(k+1) - 1

\; = (k + 1)^2
Posting by : rinrin risnawati





0 komentar:
Posting Komentar